| Medicalizing Societal Decay & The Invention of Telepathic Medicine |
|
About : Advancing The Faith Based Approach of BioEthics To Medicalize Societal Decay. Such as, mass shootings, mass homeschooling, mass overdose, mass theorization (populism,book-bans), mass divorce, mass racial/ethnic conflict & mass academic dismissal by following The Scientific Method : Towards A New Wellness Science & Standard Part I. Observation (Background): I saw ahead the social and academic trauma that comes with staying true to your interest. My family members paid a steep price for their integrity early on in our childhood years, such as suicidal attempts, disciplinary handcuffing and bullying. I was a spectator of all these, and for fear of similar retribution I dodged their level of honesty for as long as I could by pursuing academic subjects that are not aligned to me. The fear carried on in me here in the U.S, while other foreign students like me suffered more. Not too long after my arrival to the U.S.,I witnessed similar pain in newly arriving English Language Learning community members who were stuck from advancing into mainstream courses by being miscategorized as learners with disability. Their advancement was only realized in the shadows through an “underground educational hallway” when I came across over 80 newly arriving multi-generational students learning in the frigid cold at 30 degrees--crammed in a garage with no ventilation. In response to this,I founded the SCSU Read Aloud--an award winning student club which mobilized 150 volunteers to help them get mainstream using the St Cloud State University facility and the support of District 742. I found my reconciliation outside the classroom through trial and error. I observed the absence of a tailored human development framework and the intellectual segregation made possible with linear grading systems. The only alternative option was facing the (A-F) grading system which was over fitting talents with linear regression or judged right brain learning curves with left brain scale. Curious minds are not welcomed to be expressive using their respective quotient, but rather to be quiet (Audit) or get penalized early on irrelevantly. For e.g. an artistic mind should be able to sit in physics but be graded relevantly and timely. This is not only a case for discussion why I have countable F at times. It was the only option to sit with curiosity without losing immigration status. But even now in 2022/3, it's still a reality of the 1.7 million open seats in 12th grade Ethiopian national university entrance exam takers which had only 55,000 enrollment. In my argument, this is a case for bioethics to have a say in grading systems and medical sociology when you have a majority of society like mine is set up to live as a monk. In Ethiopia, the faculty of spirit is a very well understood area of stamina as the epicenter for our wellness. Who practice it full-time are found in isolation as monks, living in caves or churches setting the benchmarks through normative standards, which then contributes to activating our faculty of spirit throughout our daily walks of life. According to my societal upbringing (Ethiopia), and observations thus far, the faculty of spirit resides outside of the right side or left side of brain neurophysiology's studies which rather spearheads integrating the whole brain functioning. This led me to argue, exceptionalism depends on our faculty of spirit functioning as a stimulant–capable of altering human homeostatic condition, human performance (expanded in this statement), and human relations. I learned that applied excellence comes through a mental hike–by looping through the faculty of spirit, first by getting purposed, then by embracing talent/gift, and at last by laboring through left/right side of brain activities. Sequence matters. In other words, excellence is a function of a healthy relationship of the unseen (spirit) with the seen (brain). Or, I argue, missteps through these contributes to manufacturing societal decay. This basic statement of observation has led me to extrapolate a treatable wellness area as an ecosystem inventor. My latest invention–hypothesized benchmarks in the faculty of spirit shall contribute into our study of anatomy and physiology (proposed as Symmetric Biology), and possibly paves the way towards a new medical science and practice that I propose as an ecosystem inventor: Telepathic Medicine (TD). I observed this will not only spearhead a healing process applicable to my societal upbringing, but also universally to all humanity's well-being. It will also shed light how educational settings that are not personalized leads to manufacturing societal decay affecting human relations, performance and conditions. Such as, mass shootings, mass homeschooling, mass overdose, mass theorization (populism,book-bans), mass divorce, mass racial/ethnic conflict & mass academic dismissal!
I learned forcefully late that standing up for your integrity has wellness despite the steep unavoidable price. For me, it came with the caveat of being an urban monk. Deer and insects have been my good neighbors ever since I have been living in isolation in tents, floors and cars for years now since covid. Doing so allowed me to find healing and reconciliation to my fragmented upbringing by going knee deep until I hit or establish the thresholds for a deliberate living that monks of Ethiopia share to mainstream lifestyle. Not vilifying family, government and educators, but I only highlight how far yet these institutions are from being study based for deliberate living. Part II. Question (Definition):
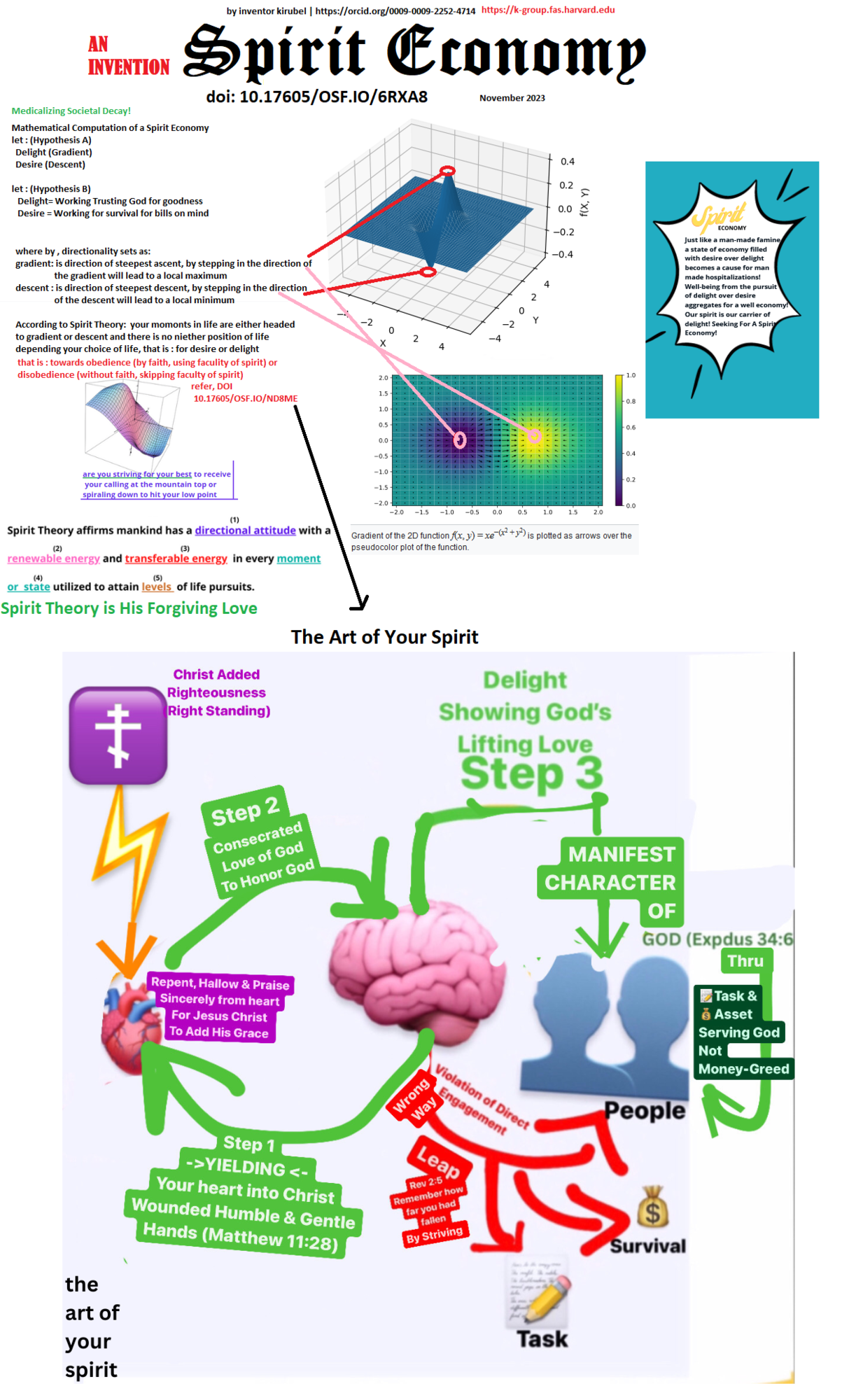
Societal decay is real as environmental decay! Societal decay generally refers to the gradual decline or deterioration of the values, norms, institutions, and overall well-being within a society. It's a concept that is often subjective and can be interpreted in various ways, depending on cultural, social, and individual perspectives. Factors contributing to societal decay may include: It's important to note that discussions about societal decay often involve subjective judgments, and different people may identify different factors as indicative of decay. Additionally, societies are dynamic, and what may be considered a sign of decay at one point in time can be addressed and improved through various means, including social, economic, and political reforms which are grounded only in normative stances. This research aims a faith based approach of standardizing (medicalizing) the normative approaches which is relied upon inconsistently and subjectively. Through bioethical frameworks and neuroscientific realms, this research effort even strives to describe when, how and why there are inconsistencies by mapping our physiological faculties, innovatively. Part III. Hypothesis (Methodology): Telepathic Medicine is an effort to medicalize societal decay. Telepathic Medicine--through time--will sit well with Osteopathic, Allopathic medicine says its ecosystem inventor : Kirubel! The chain of inventions that led to Telepathic Medicine, started with Kirubel's observations on the utility of our unrelied and unseen faculty of spirit. The living translation trial and error practices in line with the documentaion of the word spirit in the Bible, convinced him to coin: Spirit Theory. While its study and impact is missing in our biological aspects, Kirubel observed its effects are well desrving to propel us towards a new biology called Symmetric Biology. Then through this biology, and by a way of advancing the faith based approach of Bioethics, Kirubel proposes Telepathic Medicine a new medical science and practice pioneered through our faculty of spirit. By facing Jesus Christ, through the inspiration of Matthew 16:24 EOTC inspired self denial hallowing for steadfash relationship, TD helps shift sight through anyone (interaction) or anything (action) towards, what Kirubel claims, the epicenter of wellness--the faculty of spirit. The Inspiration of Matthew 16:24, EOTC Inspired Self-Deinal Hallowing For Steadfast Relationship
Its Wellness Coverage & Who it is for:
Science is about making a little dent. One area I aspire to contribute is in the area of God 1st Neuroscience under the ecosystem of Telepathic Med (while I foresee itself having contributors correlating to other physiological aspects apart from neuroscience). I aim to extract alternative wellness paradigms affecting human condition, human relations and human performance, just as the hindu contributed to western society through Yoga! In this research journey, I will be investigating the introduction of a novel therapy called —> Neuromodulated Complex Reconstructive Therapy (NCRT) for caregiving to our spirit just as Osteopathic Manipulative Therapy ( OMT) applies to our bones in Osteopathic Medicine!
Part IV. Experiment & Analysis Kirubel has a radical hands on experimentation desire and experience for the sake of advancing human condition where he first started his independent research in communication satellites as a McNair Scholar'07 [learn more]. This passion had led him to develop 14 inventions as an ecosystem inventor, assigned to IBM (2014-2019). Since then (2019+) he shifted his sector to wellness and now have developed 8 packet of open inventions [ORCID] when unpacked could unleash into more than a dozen multidisciplinary subject inventions. In the past, he had won notable research grants on his independently run research proposals (under facutly guidance). Such as sponsored by, a) Office of Research and Sponsored Programs at St Cloud State University, "UAV Flight Control : Using Voice Command & Brain Waves From EEG", where he Invoked flight commands on brain waves using EEG [demo] & [poster] b) Research grant through University of Minnesota to study Mayo Clinic's Telemedicine Program [awarded but withdrawn]. He also co-authored and collaborated in international scientific publications (proceedings) such as in World Scientific and Engineering Academy and Society [learn more] and American Association of Geographers [learn more]. He has also led a team of doctors of medicine, ai and simulation experts as a Principlal Investigator(PI) filing for high impact grants offered by CDC, Gov of Canada Wellness Innovations, & US State Department. As a former student of International Law course taught at Harvard by the globally acclaimed social scientist Dr Beth Simmons (who directed the Weatherhead Center for International Affairs at Harvard), Kirubel participated in past Harvard President Innovation Challenge with Dr Simmons [learn more]. Building up on his international law studies Kirubel had run a pilot as a US State Department Treaty visa holder to design a private enterpise system globablly via his latest invention, Spirit Economy : imagine it as a humanistic layer ahead of green economy, a public service minded faith based (God 1st) but as a self organized peace corps [learn more] contributing in-shore through obediently loving one an another and off-shore to curbing national debt through bilateral trade while also advancing harmony in cross boarder human relations. Currently, Kirubel is simulating resilience of human condition by rewiring daily routine to manifeste or live through the schema above "the art of you spirit" while going through a modality he coined : urban monk. Self explantory, i.e. by approximating a lifestyle of a monk in a city by living in tent [Yahoo News]. This simulation montiors reslience of human condition with a worst case scenario i.e. starting from nothing. In the near future, he looks forward to carrying out more simulation at a zero gravity [support now]. Why Ethiopia? Not just because of his upbringing ties, but Ethiopia being a Christian society since 4Ad, has its documented and disciplined way to live [learn more] and even have a say to human resilience as a spiritual vortex -- which could export wellness through applied sciences. While in the mean time, other spiritually guided lifestyle desitnatons like Bali, Tibit, and India have gone farther in their own right into western mainstream studies by embracing wellness practices (like yoga) through researchers and advocates. To make this advocacy come to life, please join Kirubel's campaign fundraiser below! > Support The Advocacy & the launch of new school system, new research institute & new capital network campaign at : https://His.Forgiving.Love > For direct contribution or collab by emailing: kirubel@his.forgiving.love Part IV. Qualitative Summary: Telepathic Med is about our wellness that comes from being firmly established in Jesus Christ, as our first love, (John 15)! In which apart from him, we bear no fruit. This is a divinely ordained Standard Operating Procedure (SOP) that has wellness manifestations or physiological implications throughout any of our life engagements which I observed and confirmed throughout my independent research investigation. Humbling outcomes from this investigation include suppressing PTSD, suicide, anxiety, chronic drug addiction, depression, unlocking an anointed gift expressed through skillset (1 Corinthians 12), conversion to an inner child (Matt 18:3), and most centrally being able to show the forgiving love of Christ to one another (1 Corinthians 13 fulfilling John 15:12/Matthew 22:37)...all by the name of Jesus Christ. I, myself, have benefited in outlasting my wellness predicaments experienced in the above three coverage areas, such as from overcoming chronic anxiety (condition), academic/workplace withdrawals/inconsistencies (performance), and sour / shallow / cutting interactions (relations) to name a few. This is worthy of giving a clear explanation and standard for folks who struggle to perceive God's glory from the Bible. Because the whole world is full of His glory (Isaiah 6), and there are ways to reverse-engineer from our "living translations" that are filled with His wonders and signs which can circle back to the same God in the Bible. ________________________________________ Support this independent research : > Open Inventions DOI : https://orcid.org/0009-0009-2252-4714 > Assigned Inventions : https://patents.justia.com/inventor/kirubel-z-seifu > by signing a petition at change.org: https://www.change.org/p/medicalizing-societal-decay > Press & Media : news@sssw.press |
|
Spirit Computer 1.0 
Spirit Computer 1.0 documents the humble begining observations that packs ecosystem wide inventions from Spirit Theory to Symmetric Biology. Spirit Theory -- having directionality fleshing out the wellness found in our spirit -computationally, to imply the neuroscience. e) This shall mark a new era to understand our faculty of spirit, for intentionality on wellbeing-then after, to legislate and embed actionable spirit science for our individual and collective wellbeing. Spirit Computer 1.0 now available in 40,000+ distributions worldwide, such as South Africa, Japan, U.K, Canada, Indonesia, Australia, & Sweden! Also availble on Apple, Amazon & most e-book Stores.
|
|
Humble Beginnings As documented on Yahoo News, for inventor Kirubel, this journey was about belongingness, wellness & harmony! It took covid shock-waves to take the road of my last resort in search of wellness.
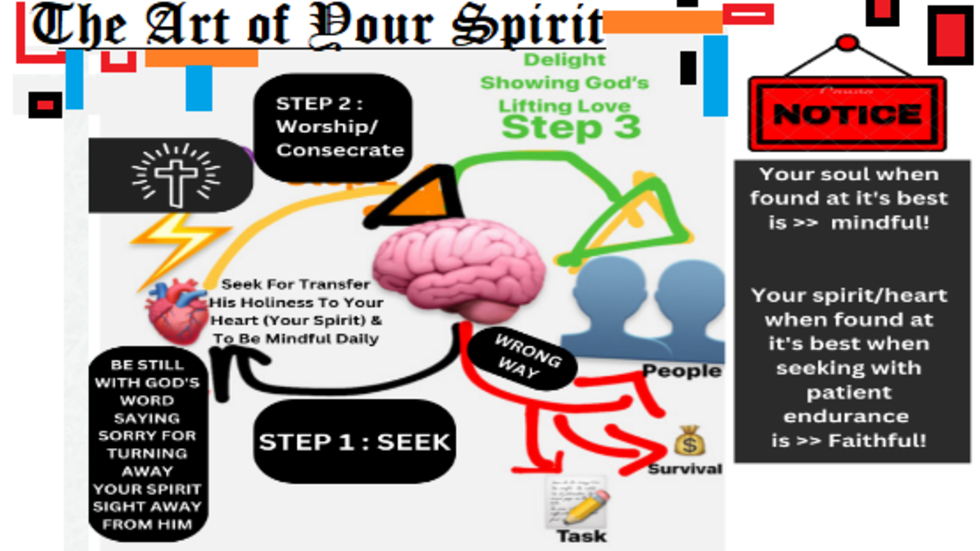
This pathway requires my full devotion to be able to sync with the lifestyle I grew up with, but which only comes with the caveat of being a full time urban monk. In becoming so, my daily routines depended on the unseen faculty found in all of us, the faculty of spirit. It has its everyday usage as being “spiritual”. According to my societal upbringing (Ethiopia), and observations thus far, the faculty of spirit resides outside of the right side or left side of brain neurophysiology's studies which rather spearheads integrating the whole brain functioning. This led me to argue, exceptionalism depends on our faculty of spirit functioning as a stimulant–capable of altering human homeostatic condition, human performance, and human relations.
|
<embed>
|
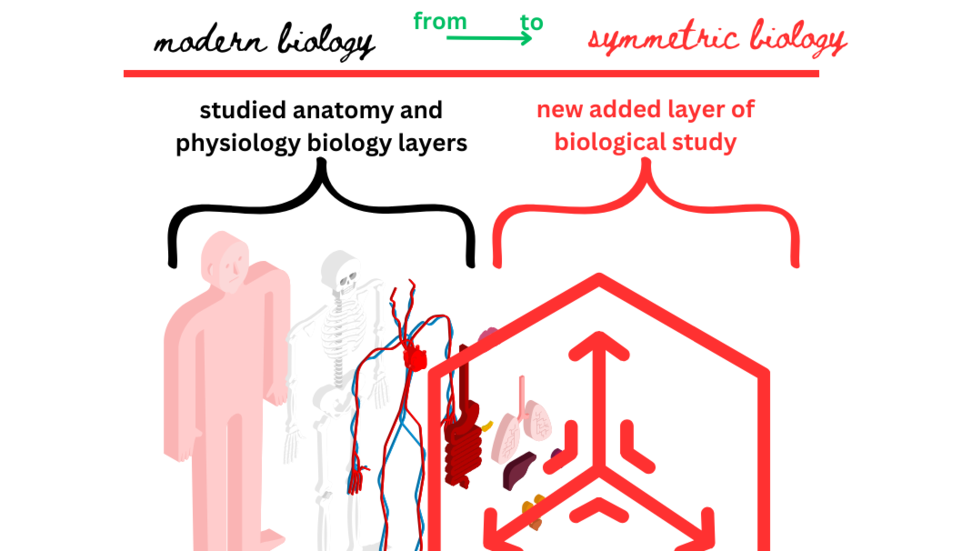
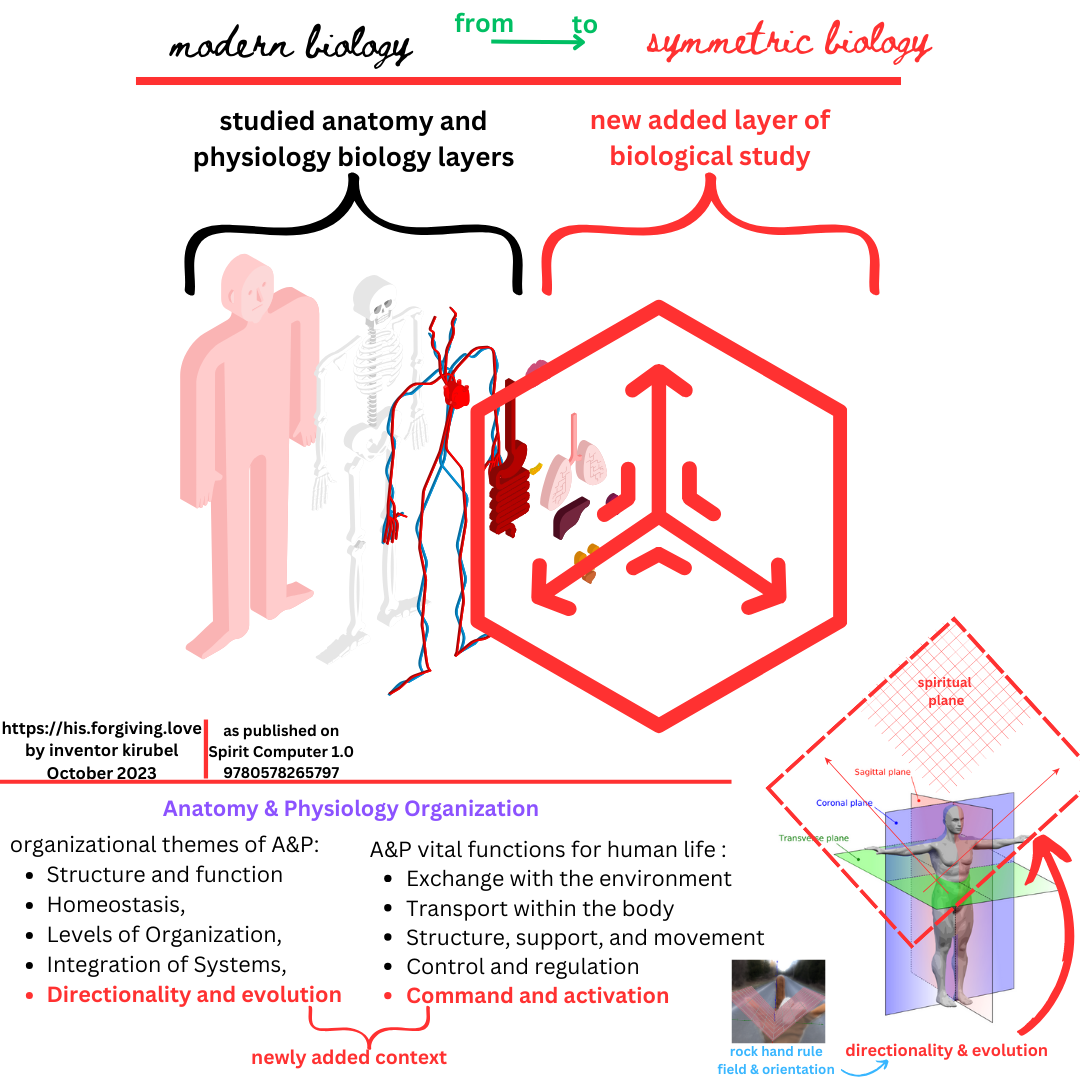
Inventions Spirit Theory : a new theory of human condition Symmetric Biology : a new layer of study ahead of Modern Biology Telepathic Medicine: a new medical science and practice medicalizing human relations, human condition, and human relations through the faculty of spirit Spirit Economy: a wellness first economy
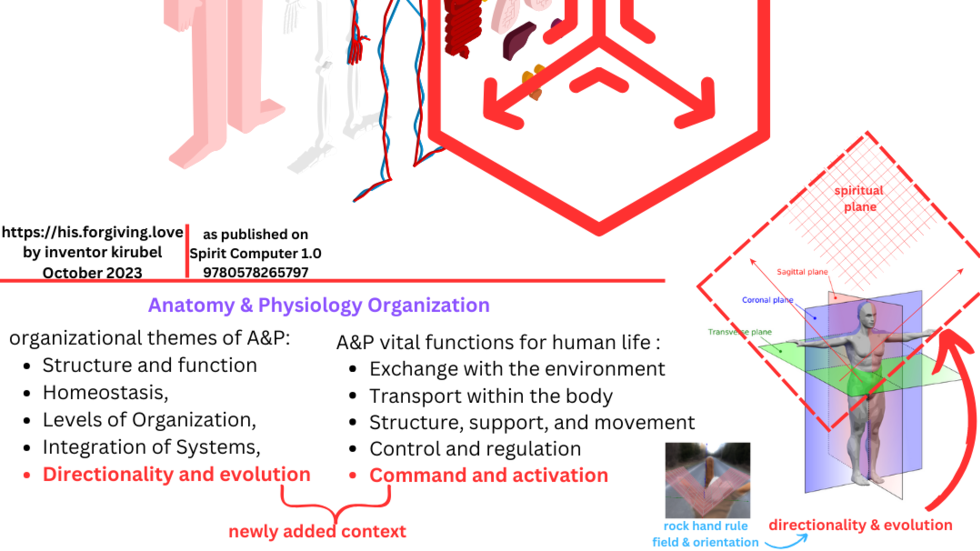
To name a few outcomes from the above inventions, looking forward to unleash additional nested inventions, such as : a new jurisprudence, telepahic messaging protocol in Systems of Systems Engineering, new genre for music therapy, quantum superpositioning of neurophysiological systems, the Leap of Faith (LoF) neurophysiological algorithm and to the Rock Hand Rule in computational geometry of directionality in high energy physics & biophyics
|
<embed>